Creating point perpendicular to the tangent of a curve?

Bug Reports / Issues
,
21

Oh, wow! Very well done! Hopefully the 1st of many :grinning:

22

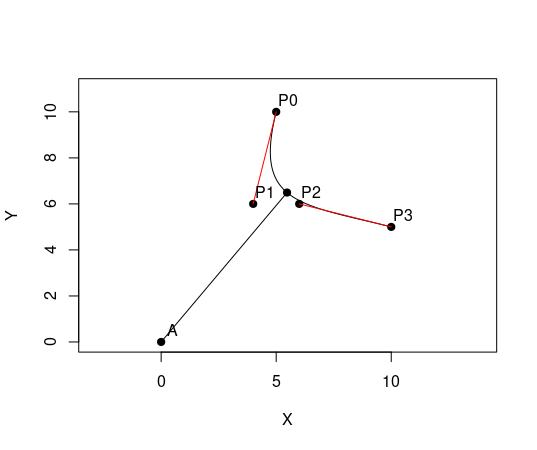
Just for fun, and knowing it is absolutely not needed, I solved the problem numerically. There is no closed analytical solution. The Bezier cubic curve is a third-order polynomial in a variable t varying between 0 and 1, and using the coordinates of the four control points as input. Its derivative is a second-order polynomial in the same variables, and the slopes of the tangents are given as Dy/Dx, where Dy is the y-derivative with respect to t, and Dx the x-derivative. The slope of the line between the axis point A and any point on the Bezier curve, can be expressed as (By - ya)/(Bx - xa), where Bx and By are the Bezier polynomials in x and y, and xa and ya the coordinates of A. Setting the multiplication of the two slopes to -1 (i.e. making them perpendicular), yields the equation: (By - ya)*Dy + (Bx - xa)*Dx =0 This is a fifth-order polynomial in t. Solving for its roots gives five complex numbers. Any of these that are real numbers are a solution to the problem. I solved the problem in R, where I had the numerical packages available. You can see a graph of an example problem included. I also include the R code for your interest. bezier.txt (1,5 KB)

afbeelding

Sometimes it is great to lose time with a little nothing…

5 Likes
23

Actually if we were to add a Curve - Perpendicular tool we would need this… but like I said at the outset, “Offhand not sure how to put that in a formula” - formula referring to the formula for the Axis angle.

Another option would be by brute force… that is to retrieve curve-> getPoints(), and then iterating from the startpoint of the curve, create a line from the current point to the axis point, check if it’s perpendicular, if so you got the point, if not continue to iterate until you’ve reached the endpoint - in which case there would be no perpendicular. Now this requires the knowledge that the app uses curves that are really made up of series of line segements, which you can easily retrieve the angle of, and thus check if the axis line is perpendicular.

2 Likes
24

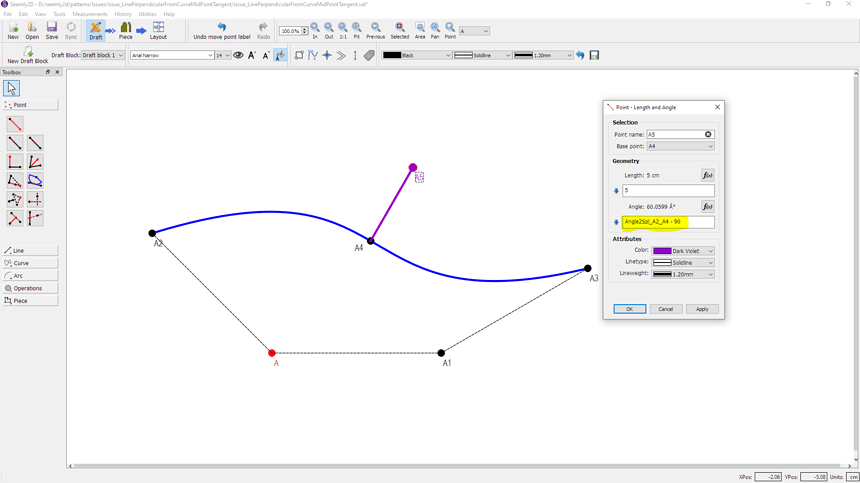
Found a way to do this.

Create the curve then use Point - On Curve tool to segment the curve with a new Point A4 . This creates two new curves that can be found using the f(x) button.
At point A4, the END angle of the FIRST new curve (or the BEGIN angle of the SECOND new curve) is the tangent angle at A4.

Create the perpendicular point A5 with the Point at Length and Angle tool, at whatever length you want and select the f(x) button to find the curve angle. In this example, select either Angle2Spl_A2_A4 or Angle1Spl_A4_A3 then add or subtract 90 degrees as needed.

issue_LinePerpendicularFromCurveMidPointTangent-1
issue_LinePerpendicularFromCurveMidPointTangent-11920×1080 118 KB

2 Likes
25

Neat, but in the OP case A5 already exists, & A4 has to dynamically shift to keep A5 at the perpendicular.

:unicorn:

2 Likes
26

DOH! That’s what I get for dropping into the conversation too late to catch the setup.

Here’s attempt #2:

Given point A and Curve C
Find B (the point on the curve where AngleLine_A_B is perpendicular to the tangent angle at B)

  1. Interpolate points along the curve B1 to B500 (500 points is probably good enough)
  2. For each point Bn, where n is 1 to 500:
    • Calculate the tangent angle at Bn
    • Calculate the line angle from Bn to A
    • If abs(tangent angle - line angle) is between 89.5 and 90.5 then FOUND else NOT FOUND # margin of error is half a degree
    • If FOUND return Bn

To interpolate a single or multiple cubic bezier segments: 

def generatePoints(curve, steps=500):
    '''
    Accepts curve points P0, C1, C2, P1 & number of steps
    steps is the number to subdivide each curve for calculating the points
    Returns array of (x, y) coordinate pairs    
    Adapted from Carlos M. Icaza www.carlosicaza.com/2012/08/12/an-more-efficient-way-of-calculating-the-length-of-a-bezier-curve-part-ii
    '''
    curve_points = []
    inc = 1    
    j = 0 
    while (j <= len(curve) - 4): #generate points for each cubic curve
        c = points2List(curve[j + 0], curve[j + 1], curve[j + 2], curve[j + 3])
        length = 0.0
        t = 0.0
        i = 0.0
        c_points = [] 
        
        while (i < steps):
            ##print '  i', i       
            t = i / steps
            # calculate point            
            t1 = 1.0 - t 
            t1_3 = t1*t1*t1
            t1_3a = (3*t)*(t1*t1) 
            t1_3b = (3*(t*t))*t1 
            t1_3c = (t * t * t) 
            ##print '  ', t, t1, t1_3, t1_3a, t1_3b, t1_3c       
            x = (t1_3 * c[0].x) + (t1_3a * c[1].x) + (t1_3b * c[2].x) + (t1_3c * c[3].x)
            y = (t1_3 * c[0].y) + (t1_3a * c[1].y) + (t1_3b * c[2].y) + (t1_3c * c[3].y)
            c_points.append((x, y))
            ##print '  x, y', pnt.x, pnt.y                  
            i += inc
            
        # append points to curve_points[]   
        curve_points.extend(c_points)
        # jump to next bezier in curve
        j = j + 3
                        
    return curve_points
1 Like
27

The issue is not how to solve for the perpendicular, but can it be put into the axis angle formula field - without creating a new tool? The answer appears to be no. We can approximate the perpendicular, but it will always vary depending on the measurements used.

2 Likes