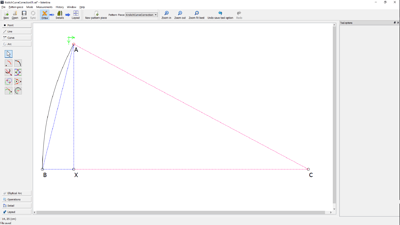
…and I’ve solved it after a good power nap with a bit of trig. I’ll explain the diagram below.
Basically, any two points on a circle (A & B) plus the center (C) form an isosceles triangle, where the CA & CB radii (and therefore the outer two angles) are equal.
Looking at the diagram, we know the angle at B (…and therefore the angle at A) and the length of AB. The angle at C is simply 180 - (A + B). What we don’t know is the length of lines AC or, FAR more importantly, as it determines the center of the arc, XC
Doing a bit of Googling to refresh my memory, I was reminded that sin(B) / AC = sin(C) / AB. As XC = AC - BX (and what we want is to place C on the line that travels through both B and X, moving things around gives me the formula XC = (AB / sin(C)) * sin(B) - XB.
As the angles are absolutes that must be turned into relatives, creating variables that do so in the background keeps everything nice and tidy, and so the formula for the length of XC is ((Line_A_B / sinD(#c)) * sinD(#b)) - Line_X_B
…except the variables table seems to explode when you use measurements to calculate things, so what I have to use is a rather unwieldy
(Line_A_B / sinD(180 - (((AngleLine_A_B - 180)) + ((AngleLine_A_B - 180))))) * sinD(AngleLine_A_B - 180) - Line_X_B. 
(Oh, yes. You MUST use ‘sinD’ instead of ‘sin’, as, while Valentina uses regular degrees for angles, the trig functions use radians by default. The ‘D’ after a trig function means it uses degrees for calculations. Forgetting the difference made me want to pull out my hair for a while there.)
It works VERY well, but, considering what a right royal pain it was to figure out and then put the formula together, I propose a tool is added to create an arc from A to B with the center along the line that includes X. (i.e. ‘Pick three points.’)
(Of course, there is still the issue that the ends of the curve(s) won’t necessarily be at the proper angle to the adjoining lines.)
Hope this helps!