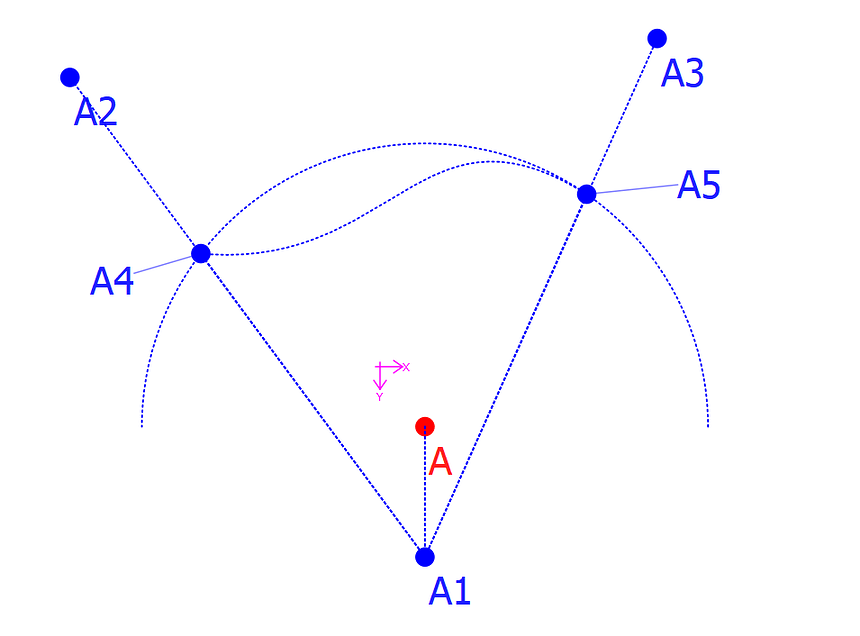
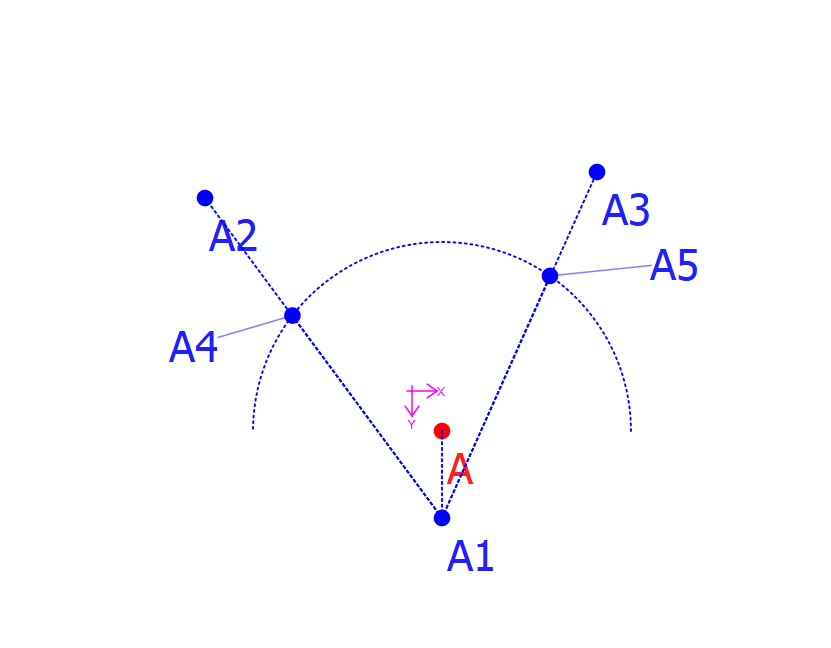
How to find middle point along arc? For very short distances I could use the MiddlePointOnLine tool. But when points on the arc are further apart, the found middlepoint will get further and further away from the actual arc line. What I have done is drawn that straight line between points and found its middle. Then using the Crossing Arc and Axis Tool to find the point on the arc. Are there other/better/faster ways to do that?
2 Likes
You can use the length of the arc divided by 2 to place a point in the centre of the arc.
2 Likes
Yes that does work. However I was trying to do something like on the example. Where A4 and A5 both lie on the same arc and I now want to find the middle point along the arc between those points. I have created an exaggerated example to help making it clear. The length if the curve between A4 and A5 isn’t known, yet I need it to divide it into parts. IN this case it could probably be done by drawing a line between A4 and A5, then drawing a line from A1 through the middle of that line. But that only goes when the arc is a perfect circle and both helper lines (A1-A4 and A1-A5) stem from the same origin. This method however fails when the circle is rather a spline. See second example. In the end I just eyeballed it. The original instructions read. Draw a smooth curve and find the middle along its path. Perfectly doable with a ruler, not so simple for me doing it electronically.
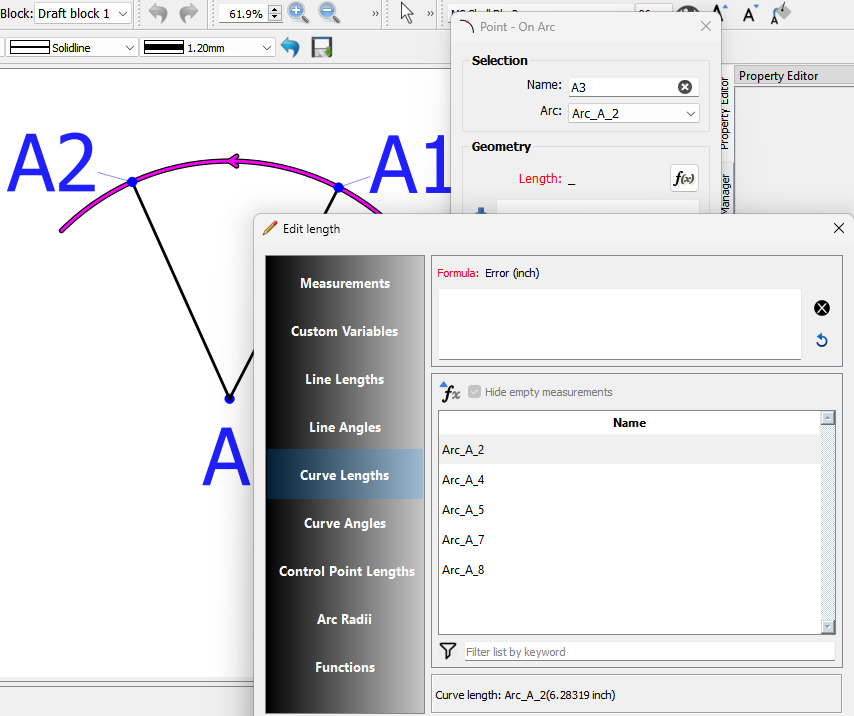
Use the
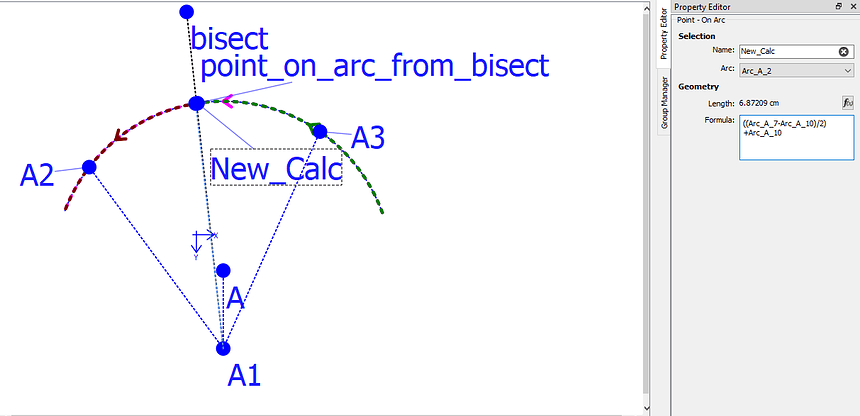
tool and in the formula use the ((length of the arc to A4 - length to A5) / 2) + length to A5.
Unfortunately you have to decipher the which curve length is which in the Variables table, as the names are not based on the point names, but rather the order in which they were created.
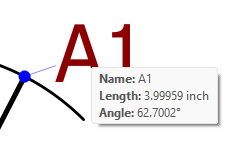
You can use the info in the rollover to figure out which length is which.
3 Likes
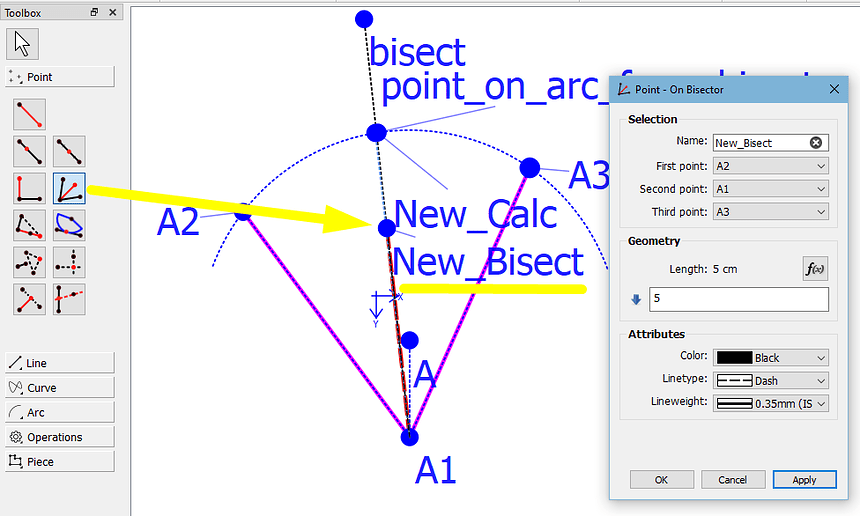
I just couldn’t get it to work. I couldn’t find the curve lengths I needed. My bad I guess. But I found a way. goes like this: Take the largest angle, substract the smaller angle. We now have the angle between the two legs. Divide that number by two and add the smaller angle. Point (length and Angle) Name {bisect} Length {line length A1-A4} Angle { ((AngleLine_A1_A4-AngleLine_A1_A5)/2)+(AngleLine_A1_A5) } It is a bit of a workaround, but at least I got it figured out and it works.
1 Like
Here is the same as @Douglas showed you, just minused off the A1 on the arc. It takes some testing to match the arc name to the nodes.
Anyway, I’m glad you found a method that works for you 
I did look again, I must have done something different as both points on the arc (A2 and A3 in my case) aren’t named in the ‘Curve lengths’. There are no other arcs in the ‘Curve lengths’ then the one named arc_A_2, being the main arc. Here’s my file… Did I miss something?? Could you please have a look? test.sm2d (1.7 KB)
2 Likes
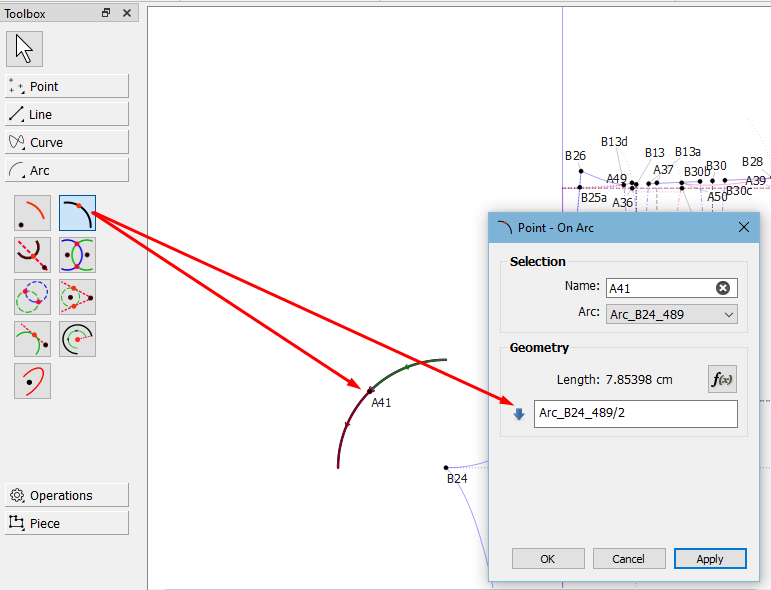
You can test the arc’s label to see which section the arc in the list belongs to by entering only 1 arc at a time and hitting Apply instead of OK. The arc section will highlight and the new node will fall on an existing node. Once you know which arc will fall on the 2 nodes needed, then you can do the rest of your formula.
And if you want to place a line between 2 lines there’s also a tool for that (just for future FYI)…
Here’s your test back so that you can see what I did…
test A.sm2d (2.1 KB)
1 Like
Yup… that works, too. 
2 Likes